蒙特卡罗方法详解

蒙特卡罗方法是由冯诺依曼和乌拉姆等人发明的，“蒙特卡罗”这个名字是出自摩纳哥的蒙特卡罗赌场，这个方法是一类基于概率的方法的统称，不是特指一种方法。

蒙特卡罗方法也成统计模拟方法，是指使用随机数（或者更常见的伪随机数）来解决很多计算问题的方法。他的工作原理就是两件事：不断抽样、逐渐逼近。下面用两个例子[1]来理解一下这个方法的思想。

（1）圆周率 $\pi$ 值求解

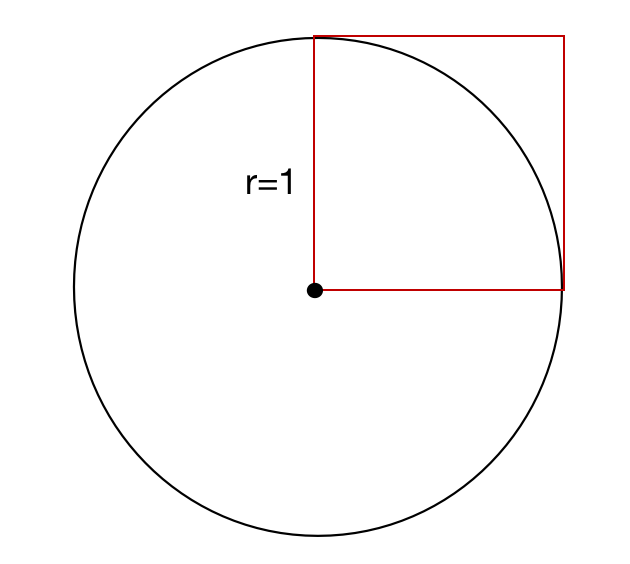
如图所示，有一个半径为r=1的圆和边长为1的正方形，圆的面积为 $\pi r^{2}=\pi$ ，则正方形内部的相切圆的面积为整个圆的1/4，也就是 $\frac{\pi}{4}$ ，正方形的面积为1。然后我们向正方形中随机打点，就会有一定的概率落在圆中：

这样我们就可以得到落在圆中的概率就是=圆的面积/正方形面积= $\frac{\pi}{4}$ ，那么就可以推出圆周率的计算公式：

$\pi = 4*落在圆中的概率=4*(红色点数/总点数)$

其中红色点可以定义为距离圆点距离小于1的点，可以通过python实现来看一下：

import random
total = [10, 100, 1000, 10000, 100000, 1000000, 5000000]  #随机点数
for t in total:
    in_count = 0
    for i in range(t):
        x = random.random()
        y = random.random()
        dis = (x**2 + y**2)**0.5
        if dis<=1:
            in_count += 1
    print(t,'个随机点时，π是：', 4*in_count/t)

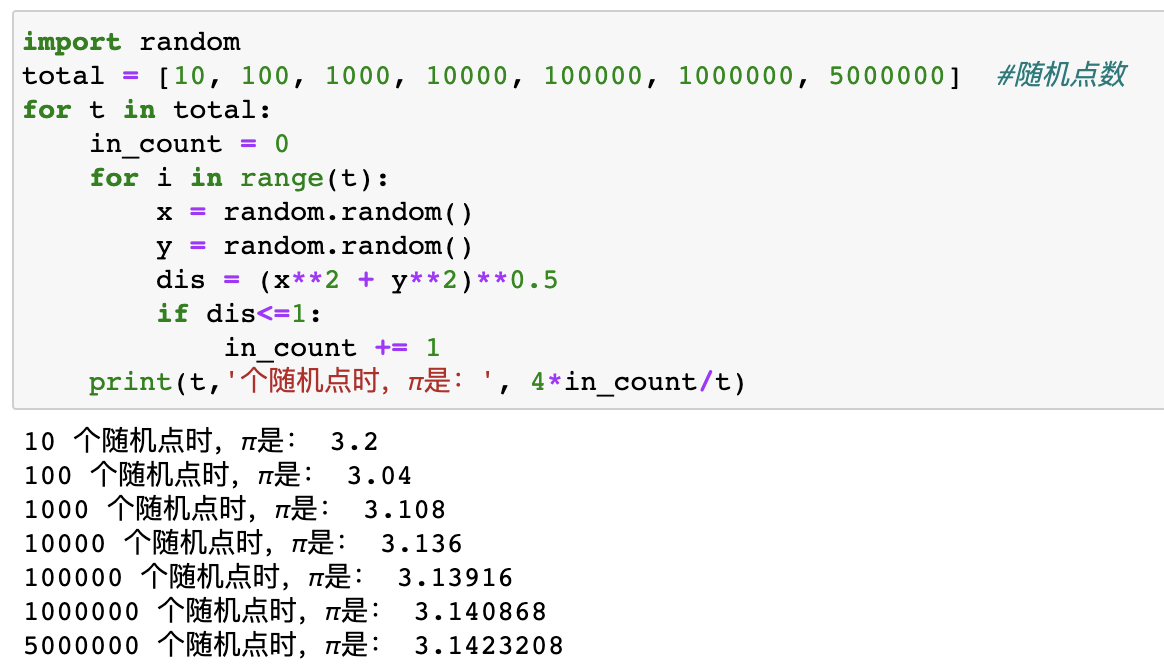
可以看出随着随机点数的增加，近似度逐渐增大。

（2）计算不规则图形面积

比如下面这张黑底图片，想要计算图中白色图形的面积，其中图形都是不规则图形，我们没办法通过边长公式等进行计算，其中一种方法就是可以通过蒙特卡罗方法，向图上随机打点，然后获取像素点所在的颜色，白色面积=白色点数/总点数*图片总面积（当然其实可以用计算机遍历所有像素点也可以求，但这里主要用来说明蒙特卡罗思想的方法）

下面还是通过python进行实现：

from PIL import Image
import random
img = Image.open('monte.png')  #读取图片
total = [10, 100, 1000, 10000, 100000, 1000000, 5000000]  #随机点数
for t in total:
    in_count = 0
    for i in range(t):
        x = random.randint(0, img.width-1)
        y = random.randint(0, img.height-1)
        if img.getpixel((x,y))==(255,255,255,255):   #数据输出格式：(R, G, B, A)
            in_count += 1
    print(t,'个随机点时，白色面积为：', int(img.width*img.height*in_count/t))

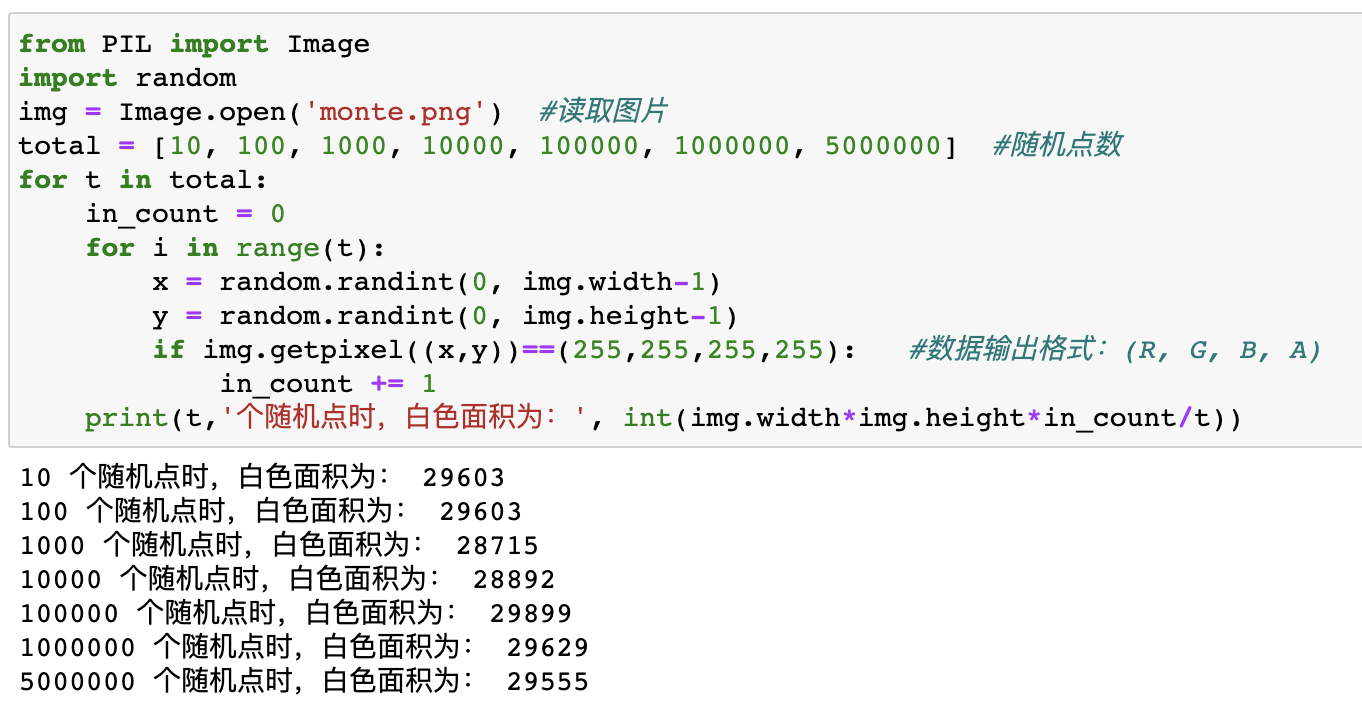
通过上面两个例子我们可以理解蒙特卡罗算法的一个基本思想，其实就是通过随机点来模拟实际的情况，不断抽样以逼近真实值。

由蒙特卡洛法得出的值并不是一个精确值，而是一个近似值，而且当投点的数量越来越大时，这个近似值也越接近真实值。

通常蒙特卡罗方法可以粗略地分成两类[2]：

一类是所求解的问题本身具有内在的随机性，借助计算机的运算能力可以直接模拟这种随机的过程。例如在核物理研究中，分析中子在反应堆中的传输过程。中子与原子核作用受到量子力学规律的制约，人们只能知道它们相互作用发生的概率，却无法准确获得中子与原子核作用时的位置以及裂变产生的新中子的行进速率和方向。科学家依据其概率进行随机抽样得到裂变位置、速度和方向，这样模拟大量中子的行为后，经过统计就能获得中子传输的范围，作为反应堆设计的依据。

另一种类型是所求解问题可以转化为某种随机分布的特征数，比如随机事件出现的概率，或者随机变量的期望值。通过随机抽样的方法，以随机事件出现的频率估计其概率，或者以抽样的数字特征估算随机变量的数字特征，并将其作为问题的解。这种方法多用于求解复杂的多维积分问题。

比如积分 $\theta=\int_{a}^{b}f(x)dx$ ，如果f(x)的原函数很难求解，那么这个积分也会很难求解。

那么我们如何通过蒙特卡罗方法对其进行模拟求解呢？

（1）随机投点法

这个方法和上面的两个例子的方法是相同的。如下图所示[3]，有一个函数f(x)，要求它从a到b的定积分，其实就是求曲线下方的面积：

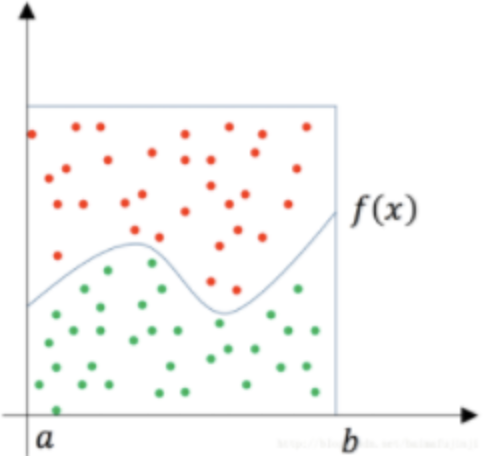
这时可以用一个比较容易算得面积的矩型罩在函数的积分区间上（假设其面积为Area），然后随机地向这个矩形框里面投点，其中落在函数f(x)下方的点为绿色，其它点为红色，然后统计绿色点的数量占所有点（红色+绿色）数量的比例为r，那么就可以据此估算出函数f(x)从 a 到 b 的定积分为 Area × r。

（2）平均值法（期望法）

如下图所示，在[a,b]之间随机取一点x时，它对应的函数值就是f(x)，我们要计算 $\theta=\int_{a}^{b}f(x)dx$ ，就是图中阴影部分的面积。

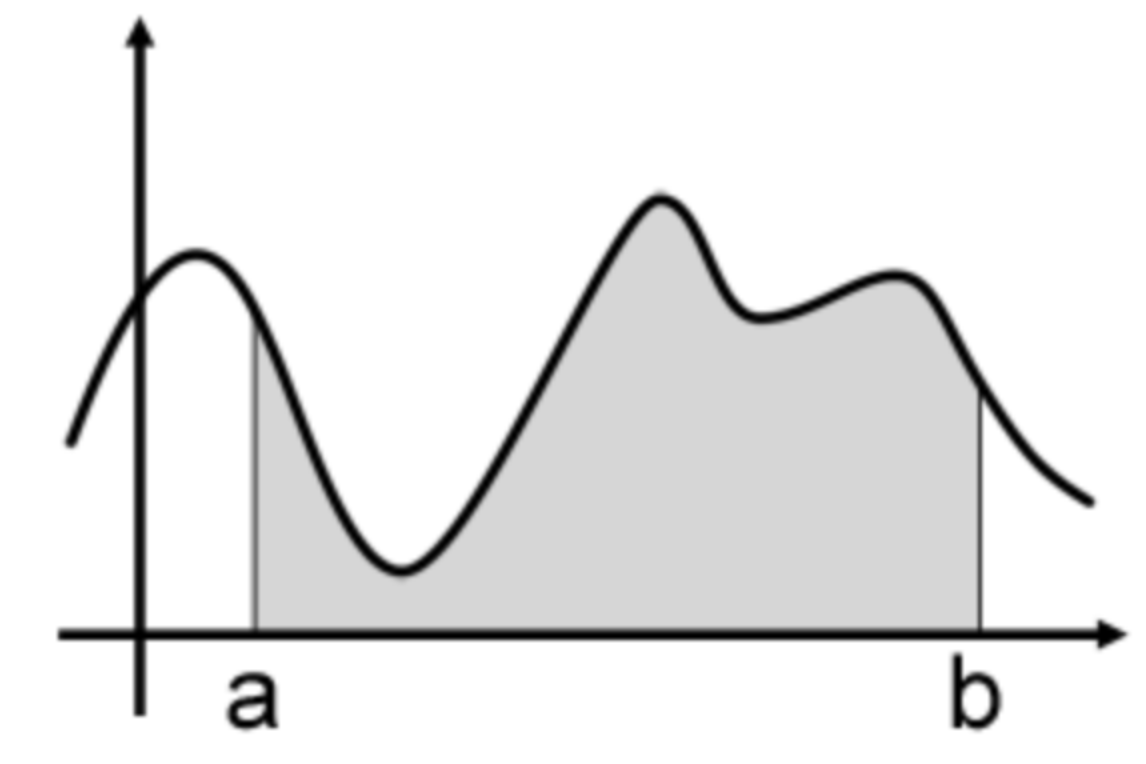
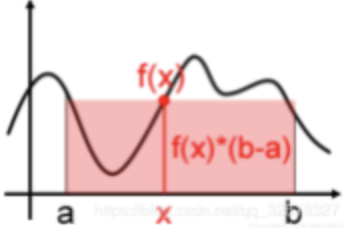
一个简单的近似求解方法就是用来粗略估计曲线下方的面积，在[a,b]之间随机取点x，用f(x)代表在[a,b]上所有f(x)的值，如下图所示：

用一个值代表[a,b]区间上所有的 ( )的值太粗糙了，我们可以进一步抽样更多的点，比如下图抽样了四个随机样本 $x_{1},x_{2},x_{3},x_{4}$ （满足均匀分布），每个样本都能求出一个近似面积值 $f(x_{i})*(b-a)$ ，然后计算他们的数学期望，就是蒙特卡罗计算积分的平均值法了。

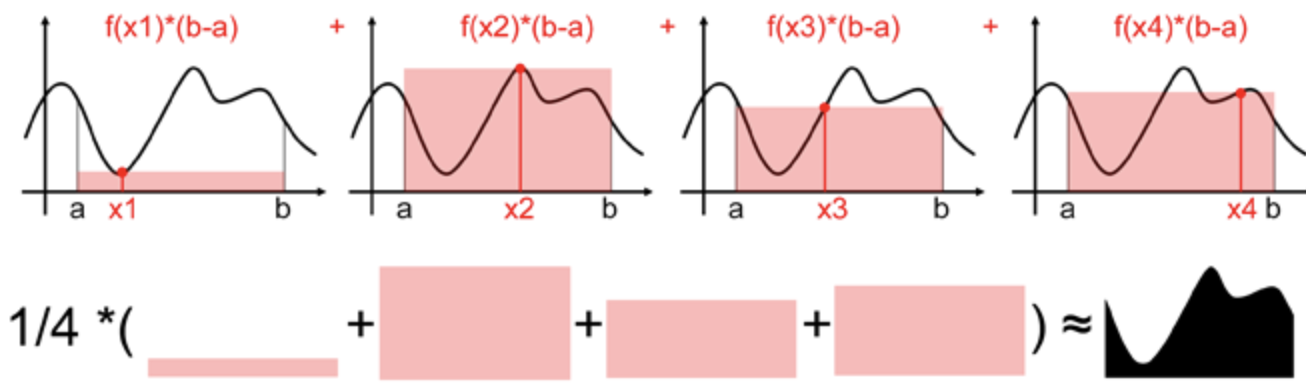
用数学公式表述上述过程：

$S=\frac{1}{4}[f(x_{1})(b-a)+f(x_{2})(b-a)+f(x_{3})(b-a)+f(x_{4})(b-a)]=\frac{1}{4}(b-a)(f(x_{1})+f(x_{2})+f(x_{3})+f(x_{4}))=\frac{1}{4}(b-a)\sum_{i=1}^{4}{f(x_{i})}$

然后进一步我们采样n个随机样本（满足均匀分布），则有：

$S=\frac{b-a}{n}\sum_{i=1}^{n}{f(x_{i})}\simeq\theta$

采样点越多，估计值也就越来越接近。

上面的方法是假定x在[a,b]间是均匀分布的，而大多时候x在[a,b]上不是均匀分布的，因此上面方法就会存在很大的误差。

这时我们假设x在[a,b]上的概率密度函数为，加入到 $\theta=\int_{a}^{b}f(x)dx$ 中变换为：

$\theta=\int_{a}^{b}f(x)dx=\int_{a}^{b}\frac{f(x)}{p(x)}p(x)dx\simeq\frac{1}{n}\sum_{i=1}^{n}{\frac{f(x_{i})}{p(x_{i})}}$

这就是蒙特卡罗期望法计算积分的一般形式。

那么问题就换成了如何从p(x)中进行采样。

蒙特卡罗采样方法：

① 常见的概率分布采样

补更：这里再更新解释一下，说的更简单一些。

在均匀分布U(0,1)中采样是十分容易通过计算机实现的，针对常见的概率分布都可以通过均匀分布来进行采样，比如下面这个正态分布（当然一般正态分布也不需要通过这种方法，就是为了更好的说明）的概率密度曲线PDF，我们绘制它的累计概率分布曲线CDF：

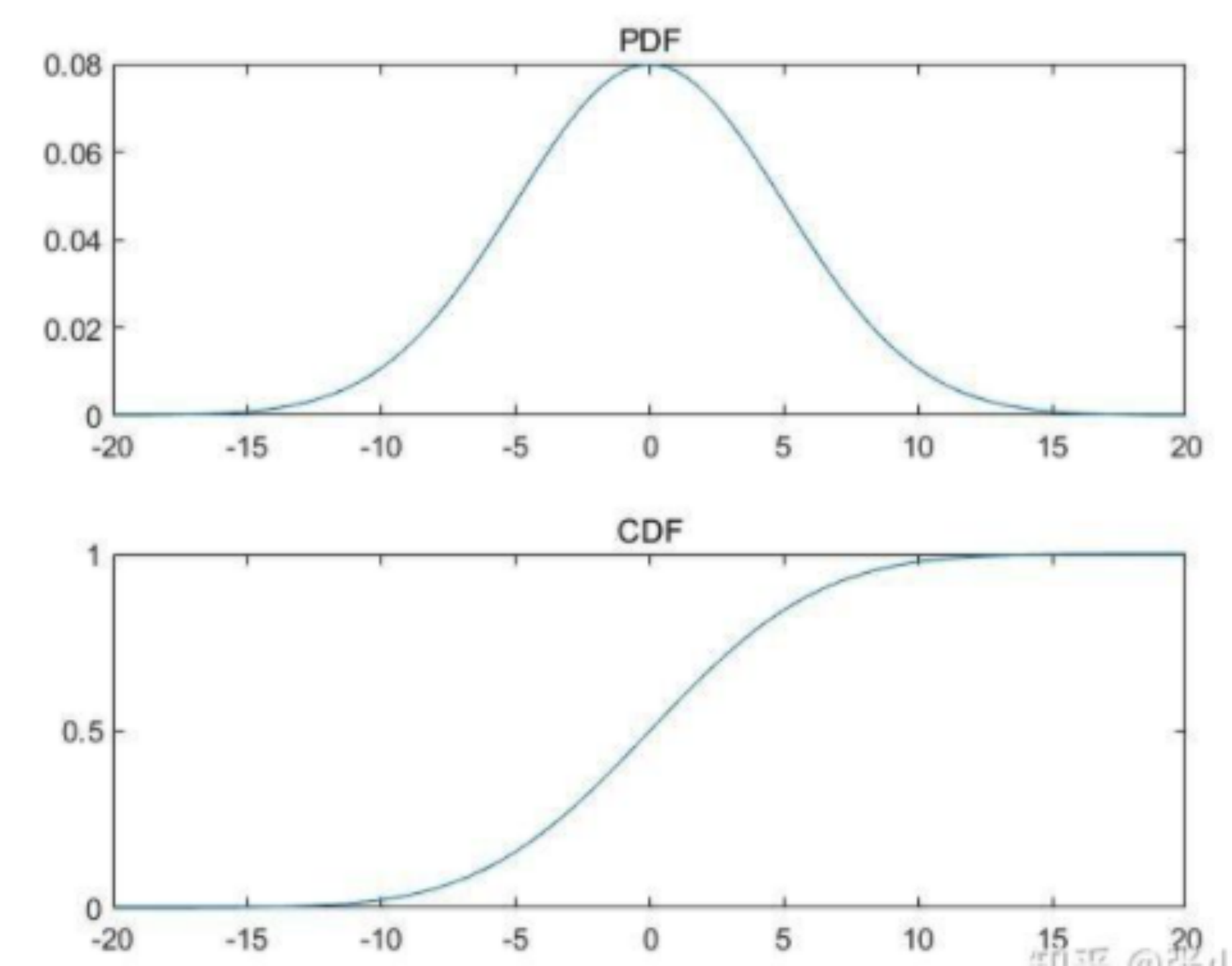
CDF曲线的纵轴是从0到1的，我们可以从均匀分布U(0,1)中采样一个点，然后计算其CDF的反函数，就能得到我们需要的样本点x：

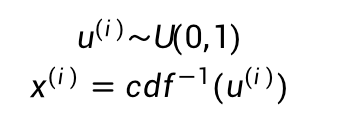
原讲解：

如果x在[a,b]的概率分布是我们常见的分布，就可以将其概率密度公式p(x)直接代入 $\theta=\frac{1}{n}\sum_{i=1}^{n}{\frac{f(x_{i})}{p(x_{i})}}$ 中然后求解。

例如在[a,b]之间是均匀分布，此时 $p(x_{i})=\frac{1}{b-a}$ ，代入上式为 (与上面推导出来的相同): $\theta=\frac{1}{n}\sum_{i=1}^{n}{\frac{f(x_{i})}{1/(b-a)}}=\frac{b-a}{n}\sum_{i=1}^{n}{f(x_{i})}$

其他常见的分布比如正态分布、t分布，F分布，Beta分布，Gamma分布等[4]，都可以通过标准均匀分布来变换生成（标准正态分布是十分容易采样样本的）。在python的numpy，scikit-learn等类库中，都有生成这些常用分布样本的函数可以使用。

举例说明，例如基于标准均匀分布来生成标准正态分布 :
设随机变量 $u_{1},u_{2}$ 独立且 $u_{1},u_{2} \sim U(0,1)$ ，那么 $z_{0}=\sqrt{-2lnu_{1}}cos(2\pi u_{2}),z_{1}=\sqrt{-2lnu_{1}}sin(2\pi u_{2})$ 独立且服从标准正态分布。
（著名的Box−Muller变换）

不过很多时候，我们的的概率密度p(x)不是常见的分布，它的形式可能非常复杂，或者p(x)是个高维的分布，样本的生成可能就很困难了。

② 接受拒绝采样

补更：这里再更新解释一下，说的更简单一些。

当待采样函数P(x)的形式十分复杂时，可以找一个简单的建议分布g(x)，并将其乘一个常数C使其全部在p(x)的上方，如下图所示，红线是我们要采样的p(x)，蓝色曲线为C*g(x):

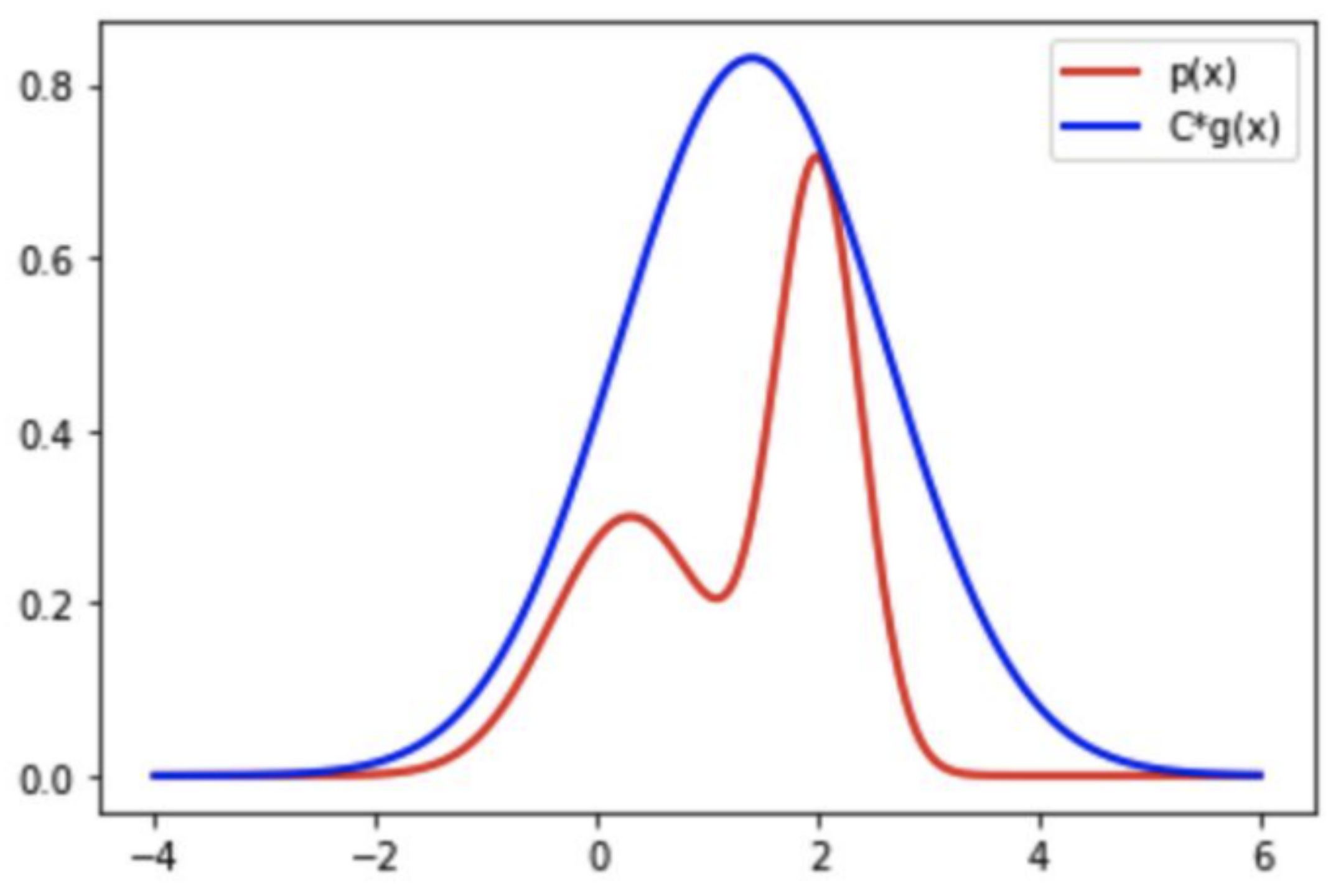
然后思路其实和前面的投点法差不多，就是从均匀分布中随机采样一个点，如果这个点在红色曲线下方，就接受它，如果在红色曲线和蓝色曲线中间，就拒绝这个点。当C*g(x)越接近q(x)时接受率越高，采样效率越高，因此有时他们差距比较大时，就会出现大部分的点都被拒绝，这样效率会非常低。

原讲解：

接受拒绝采样是一种可行的得到该分布的样本的方法，根本目标就是根据给定的概率密度函数，产生服从目标分布的样本集。[5]

采样前的准备工作：

首先需要一个辅助的建议分布(proposal distribution)，将其记做，已知其概率密度函数为。我们要由G分布来产生候选样本，因此需要我们能够从抽样，那么G抽样虽然原理上可以是任意分布，但我们应该尽量选择一个易于处理且计算机易于采样的分布，比如可以选择均匀分布、正态分布；
然后我们还需要计算一个常数值，使其对于任意变量x有 $c∗g(x)\geqslant f(x)$ ，为了提高采样效率，在满足条件的前提下常数值越小越好（当然，我们非常希望接近于1)；
还需要一个辅助的均匀分布。

真正的采样过程：

step1：从建议分布中进行采样，得到一个采样样本。
step2：从分布中进行采样，得到一个采样样本。
step3：判断，如果 $U\leqslant\frac{f(Y)}{c*g(Y)}$ ，则令（接受这个采样值），否则拒绝这个采样值，继续执行step1。

可以结合下面的这个例子来进行理解：

例如x在[a,b]上的概率分 $p(x)=\frac{1}{1.2113}(0.3exp(-(z-0.3)^2)+0.7exp(-(z-2)^2/0.3)$ ，这个概率密度函数比较复杂，下面通过接受拒绝采样进行采样。

准备：

建议分布G选择均值为1.4，方差为1.2的正态分布；
常数值C=2.5

这样建议分布G的概率密度函数的C倍是恒大于目标分布的概率密度函数p(x)的，如下图所示。

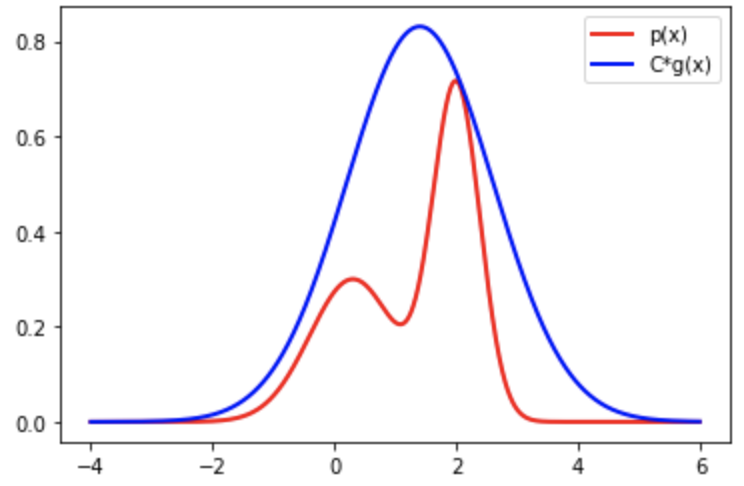
执行：

step1：从建议分布中进行采样，得到一个服从G分布的随机数Y。
step2：从分布中进行采样，得到一个服从标准均匀分布的随机数。
step3：判断，如果 $U\leqslant\frac{f(Y)}{c*g(Y)}$ ，也就是 $f(Y)\geq U*C*g(Y)$ ，这里的几何意义就是对应图中的一点在p(x)的下方，则令接受这个采样值，添加到sample列表里，否则拒绝这个采样值，继续执行step1。

最后可以看到采样点的直方图概率分布是和p(x)大致相同的：

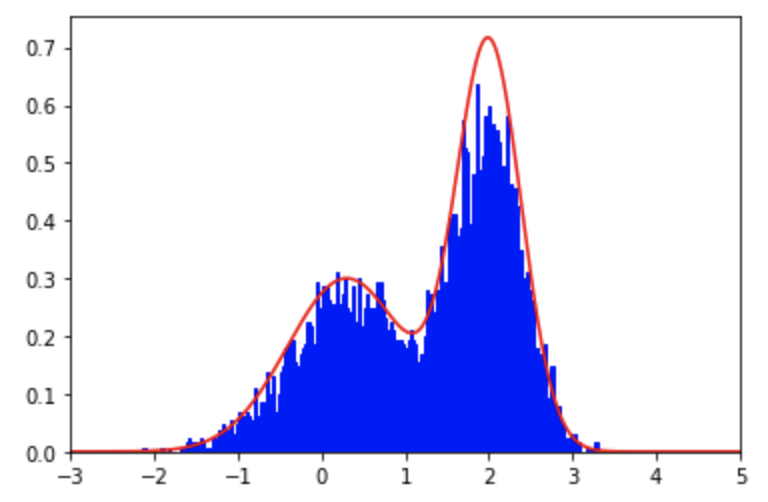
上面示例的python实现：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, uniform

#目标采样分布的概率密度函数
def p(x):
    return 0.3*np.exp(-(x-0.3)**2)+0.7*np.exp(-(x-2.)**2/0.3)

#建议分布G：选择均值为1.4，方差为1.2的正态分布
G_rv = norm(loc=1.4, scale=1.2)

#常数值C=2.5
C=2.5

#均匀分布U(0,1)
uniform_rv = uniform(loc=0, scale=1)

#绘制目标分布的概率密度函数p(x)与建议分布G的概率密度函数g(x)的C倍
x = np.arange(-4., 6., 0.01)
plt.plot(x, p(x), color='r', lw=2, label='p(x)')
plt.plot(x, C*G_rv.pdf(x), color='b', lw=2, label='C*g(x)')  #g.pdf(x)表示正态分布的概率密度函数
plt.legend()
plt.show()

sample = []
#设10000个候选采样点
for i in range(10000):
    #step1：从建议分布G中进行采样，得到服从G分布的随机数
    Y = G_rv.rvs(1)[0]   #rvs():产生服从指定分布的随机数
    
    #step2：从均匀分布 U(0,1) 中进行采样，得到服从标准均匀分布的随机数头号玩家娱乐平台
    U = uniform_rv.rvs(1)[0] 
    
    #step3：判断，如果 P(Y)≥U*C*g(Y)，则接受
    if p(Y)>=U*C*G_rv.pdf(Y):
        sample.append(Y)


#绘制目标分布的概率密度函数p(x)与建议分布G的概率密度函数g(x)的C倍
x = np.arange(-3., 5., 0.01)
plt.gca().axes.set_xlim(-3, 5)
plt.plot(x, p(x), color='r')
plt.hist(sample, color='b', bins=200, density=True, stacked=True, edgecolor='b')  #把所有直方归一化到1
plt.show()

使用接受-拒绝采样，我们可以解决一些概率分布不是常见的分布的时候，得到其采样集并用蒙特卡罗方法求和得到。

[1]【智源学院】30分钟了解蒙特卡罗方法-有意思专题系列（蒙特卡洛方法）（Monte Carlo method）_哔哩哔哩蒙特卡罗(゜-゜)つロ干杯~-bilibili

[2]小白都能看懂的蒙特卡洛方法以及python实现_bitcarmanlee的博客-CSDN博客_蒙特卡洛

蒙特卡罗

[3]蒙特卡洛方法的理解、推导和应用_氢键H-H-CSDN博客_蒙特卡洛积分推导

[4]Eureka：马尔可夫链蒙特卡罗算法（MCMC）

蒙特卡罗

[5]如何理解蒙特卡洛方法的接受拒绝采样？

一	二	三	四	五	六	日
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

蒙特卡罗：蒙特卡罗方法详解